Graphics:Angle: Difference between revisions
No edit summary |
m sp |
||
| Line 7: | Line 7: | ||
[[Image:3d_angle_improved.png]] | [[Image:3d_angle_improved.png]] | ||
The | The “giant scary eye” represents our view on to the game world. If an object in the game world has a depth '''z''' then the eye sees it vertically compressed with a height '''z'''' (shown by the red line in the diagram). Similarly, an object's height '''y''' will be vertically compressed to '''y''''. Since we use an isometric view there is no scaling in the horizontal dimension, so an object's width '''x''' will remain unchanged. The amount by which '''z''' and '''y''' need to be scaled is dependent on the angle '''A''' at which the eye looks down on the world. Some simple trigonometry yields the following formulae: | ||
'''z'''' = sin('''A''') * '''z''' | '''z'''' = sin('''A''') * '''z''' | ||
| Line 13: | Line 13: | ||
'''y'''' = cos('''A''') * '''y''' | '''y'''' = cos('''A''') * '''y''' | ||
The Adonthell Engine does not mandate any particular viewing angle, so it is up to the designers of a game to choose one. For the official Adonthell games such as | The Adonthell Engine does not mandate any particular viewing angle, so it is up to the designers of a game to choose one. For the official Adonthell games such as “[[Tasks:Road_Map#Dun_Barethsol|Dun Barethsol]]” we have agreed on an angle of 41.8 degrees. It may be an odd sounding angle, but it gives some rather convenient scaling factors when plugged into the above formulae: | ||
'''z'''' = 2/3 * '''z''' | '''z'''' = 2/3 * '''z''' | ||
'''y'''' = ~ 3/4 * '''y''' (it's actually 0.7454... but | '''y'''' = ~ 3/4 * '''y''' (it's actually 0.7454... but that’s as good as 0.75) | ||
== Examples/Guidelines == | == Examples/Guidelines == | ||
Revision as of 13:02, 9 August 2009
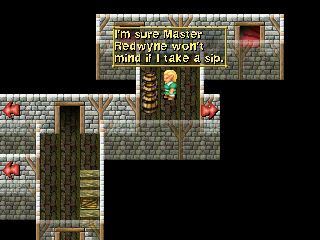
The game world is displayed by the Adonthell Engine as if it was viewed diagonally from above at a certain angle. Furthermore, the view is isometric so objects that are further away from the viewer do not appear smaller. The screenshot below illustrates this:
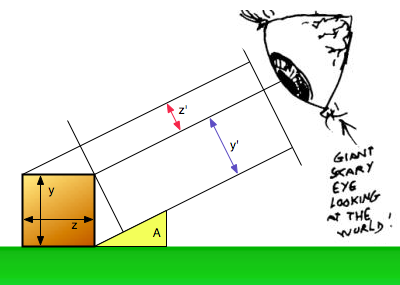
Since all the graphics in the game are just 2D bitmaps and not rendered in real-time 3D, it is up to the artists to create the illusion of a 3 dimensional world. To that end you need to decide from which angle you are looking down at the game world and design your graphics accordingly. The following diagram illustrates how the angle affects the vertical scaling of objects by taking a side-on view of the game world (imagine stepping into the game and looking at things from the left):
The “giant scary eye” represents our view on to the game world. If an object in the game world has a depth z then the eye sees it vertically compressed with a height z' (shown by the red line in the diagram). Similarly, an object's height y will be vertically compressed to y'. Since we use an isometric view there is no scaling in the horizontal dimension, so an object's width x will remain unchanged. The amount by which z and y need to be scaled is dependent on the angle A at which the eye looks down on the world. Some simple trigonometry yields the following formulae:
z' = sin(A) * z
y' = cos(A) * y
The Adonthell Engine does not mandate any particular viewing angle, so it is up to the designers of a game to choose one. For the official Adonthell games such as “Dun Barethsol” we have agreed on an angle of 41.8 degrees. It may be an odd sounding angle, but it gives some rather convenient scaling factors when plugged into the above formulae:
z' = 2/3 * z
y' = ~ 3/4 * y (it's actually 0.7454... but that’s as good as 0.75)
Examples/Guidelines
- A real world 1x1 meter square that is lying flat on the ground would result in a 64x48 pixel in-game tile.
- A 2 meter high wall, would result in a 96 pixel high sprite.
- While the game does not enforce a tile structure in the maps, keeping images as multiple of 64x48 makes it easier to combine them without gaps.
- Characters are drawn in a mild deformed style, with the body having a total height of four heads, similar to some toys such as Playmobil.